note of capacitor in circuit

 

Unit 10 : Capacitor in circuit

 

Capacitors (originally called electrical condensers) are analog electrical components that can collect and store electrical energy not electrical charge.

Capacitor can store energy quickly and can release energy quickly.

As a direct current flows into a capacitor, it charges with energy and releases an alternating current flow back into the circuit.Most capacitors have a positive and negative terminal.

Working principle of capacitor:

let us consider a parallel plate capacitor with a dielectric between them as shown in the below circuit. Now, apply the voltage V as shown in the circuit, plate 1 has the positive charge and plate 2 has negative charge. Across the capacitor an electric field appears. When these plates are applied with the voltage they will carry positive charge from the battery at plate 1 and negative charge on plate 2. For some time the voltage is applied and within that time the capacitor gets charged to the maximum limit of holding charge and this time is called as charging time of the capacitor.

 

 

 

 

 

After some time when the capacitor has reached its maximum limit of charging then we will cut the supply of power to the capacitor. For a certain time, the two plates hold a negative and positive charge. Thus, the capacitor acts as a source or electric charge

 

Capacitor in Series:

 

Series capacitors are more effective on distribution circuits with higher X/R ratio and for load variations involving a higher reactive content.

Capacitors connected in series. The magnitude of the charge on each plate is Q, C is capacitor and V is Voltage.

 

Series connections produce a total capacitance that is less than that of any of the individual capacitors. It is a general feature of series connections of capacitors that the total capacitance is less than any of the individual capacitances.

 

 

 

 

We can find an expression for the total capacitance by considering the voltage across the individual capacitors shown in Figure.

 

Q= CV …. (Chage from capacitor C and Voltage V )

 

 

Solving C= ^Q

V

 

 

for V gives v =

Q

. The voltages across the individual capacitors are

 

 

 

 

The total voltage is the sum of the individual voltages:

V=V1+V2+V3

 

Now, calling the total capacitance CS for series capacitance, consider that

 

V=^Q =V1+V2+V3

C

 

Entering the expressions for V1, V2, and V3, we get

 

Q= Q  +  Q   + Q

C      C1          C2       C3

Canceling the Qs, we obtain the equation for the total capacitance in series C to be

 

 

1= 1  +   1   + 1

C      C1          C2        C3

 

Total Capacitance in Series, Cs

 

Total capacitance in series: 1= ¹ +  1     + 1

C      C1          C2         C3

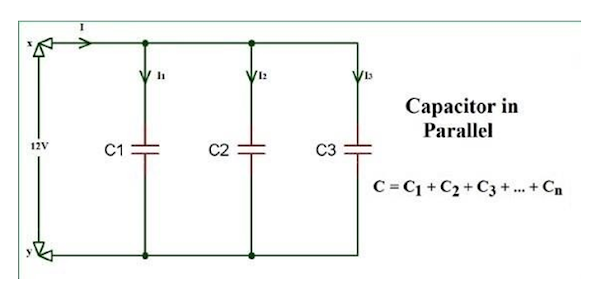
Capacitors in Parallel

 

 

 

 

 

 

 

 

Capacitors in parallel refer to the capacitors that are connected together in parallel when the connection of both of its terminals takes place to each terminal of another capacitor.

When capacitors are connected together in parallel the total or equivalent capacitance, CT  in the circuit is equal to the sum of all the individual capacitors added together. This is because the top plate of capacitor, C1  is connected to the top plate of C2  which is connected to the top plate of C3  and so on.

 

 

 

 

Using the relationship Q=CV, we see that the total charge is Q=CV

and the individual charges are Q1=C1V, Q2=C2V, and Q3=C3V. Entering these into the previous equation gives

 

 

CV = C1 V + C2 V + C3V

Canceling V from the equation, we obtain the equation for the total capacitance in parallel

 

 

C = C1 + C2 + C3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Prepared by :Mausham aryal